A Brief Introduction to Reinforcement Learning

Computational models that are implemented, i.e., written out as equations or software, are an increasingly important tool for the cognitive neuroscientist.  This is because implemented models are, effectively, hypotheses that have been worked out to the point where they make quantitative predictions about behavior and/or neural activity.

In earlier posts, we outlined two computational models of learning hypothesized to occur in various parts of the brain, i.e., Hebbian-like LTP (here and here) and error-correction learning (here and here). The computational model described in this post contains hypotheses about how we learn to make choices based on reward.

The goal of this post is to introduce a third type of learning: Reinforcement Learning (RL).  RL is hypothesized by a number of cognitive neuroscientists to be implemented by the basal ganglia/dopamine system.  It has become somewhat of a hot topic in Cognitive Neuroscience and received a lot of coverage at this past year’s Computational Cognitive Neuroscience Conference.

What exactly is RL?

RL has been succinctly defined as “the computational theory of learned optimal action control” (Daw, Niv & Dayan, Nature Neuroscience 2005).   Unpacking this a little, RL is a general term for a class of algorithm that allows an agent to select “actions” in various situations that is predicted, given past experience, to lead to the most numerical “reward”.

Reward is a key concept that differentiates RL from other applications in which neural networks are typically applied.  In typical applications, neural networks are used for:

•    pattern recognition, i.e., map an input pattern to a particular target pattern (e.g., matching a face to a name, or a pattern to a number)
•    pattern categorization, i.e., distinguishing between male or female faces (e.g., matching a face to a categorization label)
•    sequence learning, i.e., mapping a sequence of input to a prediction of future input (e.g., guessing the next word in a language stream).

In contrast, RL methods generally map an input, which can represent either an action (e.g. physical movement) or reachable state (e.g., a particular location) to a numerical value known as a reward prediction.

Reward prediction is meant to represent how “good” the input is: formally, it is the sum of all rewards expected from a particular state.  For example, a state closer to a goal will typically have a higher value than one far away from a goal.  A state close to the goal but separated from it by an impassable obstacle can have a very low value.

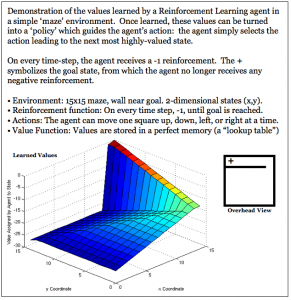
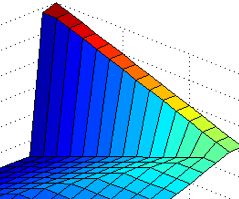
The figure box below illustrates how a simple problem can be solved using RL.  In the problem, an RL agent was given the task of reaching the corner of a simple maze as quickly as possible.  One way to translate this “task” into RL is to say that the agent receives a -1 reinforcement for every move it makes until it reaches the goal state, and it must always move. (The maze is called a maze because it has a wall near the goal to make things interesting. The agent has to learn to go around the wall.)

Reward predictions can be learned in a number of ways; one way is to iteratively update the value of each state based on the value of the best subsequent state and the immediate reward obtained on the way there (e.g., Value Iteration, Sutton & Barto, 1998).   This update rule can be derived from the formal definition of reward prediction (as shown in the equations below).

After learning, an RL Agent that is set to operate optimally can use these learned values in order to decide what action to take (or what state to enter): it just moves to the state with the next highest value.  This translates to “moving uphill” in the colorful plot shown above.

How does this relate to the brain?  It’s still a bit early to say definitively, but based on findings from fMRI, neurophysiology and neuroanatomy, theoreists have suggested that something like RL might be implemented in the basal ganglia/dopamine system (e.g., Doya, Neural Networks, 2002).

This was just a brief introduction to the concepts of Reinforcement Learning; good starting points for more detailed information are the Scholarpedia page on Reinforcement Learning and the 1998 textbook by Sutton and Barto entitled “Reinforcement Learning: An Introduction” (available online here).

-P.L.