 Backpropogation of Error (or "backprop") is the most commonly-used neural network training algorithm. Although fundamentally different from the less common Hebbian-like mechanism mentioned in my last post , it similarly specifies how the weights between the units in a network should be changed in response to various patterns of activity. Since backprop is so popular in neural network modeling work, we thought it would be important to bring it up and discuss its relevance to cognitive and computational neuroscience. In this entry, I provide an overview of backprop and discuss what I think is the central problem with the algorithm from the perspective of neuroscience.
Backpropogation of Error (or "backprop") is the most commonly-used neural network training algorithm. Although fundamentally different from the less common Hebbian-like mechanism mentioned in my last post , it similarly specifies how the weights between the units in a network should be changed in response to various patterns of activity. Since backprop is so popular in neural network modeling work, we thought it would be important to bring it up and discuss its relevance to cognitive and computational neuroscience. In this entry, I provide an overview of backprop and discuss what I think is the central problem with the algorithm from the perspective of neuroscience.
Backprop is most easily understood as an algorithm which allows a network to learn to map an input pattern to an output pattern. The two patterns are represented on two different "layers" of units, and there are connection weights that allow activity to spread from the "input layer" to the "output layer." This activity may spread through intervening units, in which case the network can be said to have a multi-layered architecture. The intervening layers are typically called "hidden layers".
Each unit in a backprop network sums up the activity coming into it through its weights and applies a "non-linearity" to it. The units used in backprop have continuous output values ranging from 0 to 1, althought for a range of inputs the activity of each unit tends to be near 0 or 1. In this sense, these units are similar (but not identical) to the McCulloch-Pitts 0 or 1 neurons described earlier.
Let's give our network a task — to display an "O" in its output units when an "X" is present on its inputs. We'll imagine that each layer is arranged to form a 2D square of, say, 20 x 20 units.
If you activate the units on the input layer with a particular pattern, such as the shape of the letter "X", the activity will feed forward through connections (and possibly other layers of units) until it reaches the output layer and will generate a pattern there. Since networks are usually initialized with random weights, before any learning has taken place, that output pattern will likely be a random pattern instead of the desired pattern, our "O".
Backprop states that one should compute the unit-by-unit "error" at the output layer by subtracting the actual output activity of each unit from the desired output activity. Then, going through the entire network, the weight connecting each unit to another should be changed in negative proportion to the error they caused on the output layer.
For example if a dot in the middle of the input "X" happened to cause an output unit to have an undesired pixel in the center of the "O", the weights leading through the network to that output unit will be weakened. (The learning rate is a number that specifies the maximum amount by which a weight can be changed in one simulation step; it is usually small to prevent weights from going to zero or too far past their ideal values in a single step. By the way, it should probably really be called synaptic modification rate because it is not directly related to the speed at which the network as a whole learns.)
On the other hand, if an output unit wasn't active that should have been, i.e. to make the "O" outline, weights to that unit from this central "X" pixel will be strengthened. So that's the basic idea behind backprop. It's only a tiny bit more complicated than this: to figure out exactly how much any particular weight should be changed — especially since there may be several layers of intervening weights — the "chain rule" from calculus is used. The chain rule allows backprop to take into account how the changes in all the weights combine.
Backprop has been used to train networks in a variety of cognitive tasks. Examples range from categorizing stimuli, recognizing the gender of human faces (with better accuracy than humans according to Gray, Lawrence, Golomb & Sejnowski!), determining syntactic and semantic categories from context (Elman, 1991), and even learning to play harmonic second voices in real-time.
Unfortunately, from the perspective of cognitive neuroscience, backpropogation is problematic for several reasons — too many, in fact, to go into in a single entry. Here I'll focus on one: backprop relies on an assumption that has not been shown to be biologically realistic.
The problematic assumption is that there is non-local computation occuring in backprop. If 3 neurons are connected in this way: A->B->C, and activating A caused an "error" in C, then backprop says that not only does the B->C weight change, but so does the A->B weight in proportion to the error at C. There is no evidence that this occurs in the brain.
In contrast, the temporally-asymmetric Hebbian-learning discussed previously is based on completely local synaptic modification processes that have been demonstrated in biology such as LTP (Levy & Steward, 1983).
Now, perhaps backprop is approximating some process that is actually at work in real neural systems. It is possible that the brain uses its arsenal of recurrent connections, inhibitory interneurons, etc., to emulate this powerful yet spooky "synaptic weight change at a distance"…. however, such a phenomenon remains to be shown experimentally. Backprop would be much easier for the common neurscientist to accept if a neurophysiologist could demonstrate real synapses where this kind of process occurs.
In the meantime, backprop continues to be used today (especially by the more imaginative modelers) for several reasons. First, it works. Second, its mathematics and properties are pretty well understood. Third, it is already in widespread use and is generaly considered acceptable by journals. To paraphrase a modeler who uses backprop and whom I greatly respect, "We know that backprop is not realistic… but we use it in the hopes that the connections it learns are similar to the kinds of connections used in the brain."
-PL
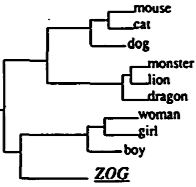
About the Figure: The figure shows some of the semantic categories discovered by Elman's version of a Jordan (1986) network (Elman, 1991) which was trained using backprop. Interestingly, the network was trained (using backprop) to simply predict the upcoming word in a sequence. The activities of the units in the intermediate "hidden" layer were grouped according to similarity, which generated the figure. When the word ZOG was shown in contexts similar to other subjects (e.g. boy, girl, dog), the network internally represented ZOG similarly to boy and girl, but differently from inanimate objects like "plate" and "glass".
hi,
can you give me a reference for your following claim?
«and even learning to play harmonic second voices in real-time.»
it would interest me.
thank you,
stefano
Stefano,
Although I cannot remember the reference I had seen a few years ago, I was able to find an article in the “Proceedings of the International Computer Music Association”. The reference is:
Gang, D., Lehmann, D. (1998) “Tuning a Neural Network for Harmonizing Melodies in Real-Time”. Proceedings of the International Computer Music Association.
Try http://citeseer.ist.psu.edu/gang98tuning.html for the text. The article describes the recurrent neural network and how it was trained.
I’m fairly sure the paper I had originally seen was in a journal in 2000 or so… if I run across it I will let you know.
-PL
This is a good post, summarizing the field’s general take on backpropagation.
You should look at the generalized recirculation algorithm, GeneRec, in O’Reilly and Munakata’s 2000 textbook. It essentially performs backprop, using only information local to each synapse. It gets information about error to each synapse by allowing the network to settle into a state constituting a “guess” as to the outcome, followed by a separate state that involves the correct output. Feedback and lateral connections ensure that the whole net is in a different state when correct output information is present. The learning rule then pushes weights toward the correct state, and away from the guess state. The learning rule at local synapses is very similar to the experimentally observed role of calcium influx at each synapse. Also, the algorithm seems to continue to work with very asymmetric connections, and would likely work without reciprocal connections between every individual unit.
This approach seems to solve the biological plausibility side of the error-driven learning puzzle. The remaining question, and one that must be answered by most forms of learning rule is this: where does the correct output information come from? I don’t think that anyone has fully thought through what information people actually use to learn from.